from IPython.display import Image
Image('../../Python_probability_statistics_machine_learning_2E.png',width=200)
It is sometimes very difficult to unequivocally attribute outcomes to causal factors. For example, did your experiment generate the outcome you were hoping for or not? Maybe something did happen, but the effect is not pronounced enough to separate it from inescapable measurement errors or other factors in the ambient environment? Hypothesis testing is a powerful statistical method to address these questions. Let's begin by again considering our coin-tossing experiment with unknown parameter $p$. Recall that the individual coin-flips are Bernoulli distributed. The first step is to establish separate hypotheses. First, $H_0$ is the so-called null hypothesis. In our case this can be
$$ H_0 \colon \theta < \frac{1}{2} $$and the alternative hypothesis is then
$$ H_1 \colon \theta \geq \frac{1}{2} $$With this set up, the question now boils down to figuring out which hypothesis the data is most consistent with. To choose between these, we need a statistical test that is a function, $G$, of the sample set $\mathbf{X}_n=\left\{ X_i \right\}_n $ into the real line, where $X_i$ is the heads or tails outcome ($X_i \in \lbrace 0,1 \rbrace$). In other words, we compute $G(\mathbf{X}_n)$ and check if it exceeds a threshold $c$. If not, then we declare $H_0$ (otherwise, declare $H_1$). Notationally, this is the following:
$$ \begin{align*} G(\mathbf{X}_n) < c & \Rightarrow H_0 \\\ G(\mathbf{X}_n) \geq c & \Rightarrow H_1 \end{align*} $$In summary, we have the observed data $\mathbf{X}_n$ and a function $G$ that maps that data onto the real line. Then, using the constant $c$ as a threshold, the inequality effectively divides the real line into two parts, one corresponding to each of the hypotheses.
Whatever this test $G$ is, it will make mistakes of two types --- false negatives and false positives. The false positives arise from the case where we declare $H_0$ when the test says we should declare $H_1$. This is summarized in the Table 1.
$$ \begin{table} \footnotesize \centering \begin{tabular}{l|p{1.3in}|p{1.3in}} \multicolumn{1}{c}{ } & \multicolumn{1}{c}{Declare $H_0$ } & \multicolumn{1}{c}{ Declare $H_1$ } \\ \hline $H_0\:$ True & Correct & False positive (Type I error) \\ \hline $H_1\:$ True & False negative (Type II error) & Correct (true-detect) \\ \hline \end{tabular} \caption{Truth table for hypotheses testing.} \label{tbl:decision} \tag{1} \end{table} $$ For this example, here are the false positives (aka false alarms): $$ P_{FA} = \mathbb{P}\left( G(\mathbf{X}_n) > c \mid \theta \leq \frac{1}{2} \right) $$ Or, equivalently, $$ P_{FA} = \mathbb{P}\left( G(\mathbf{X}_n) > c \mid H_0 \right) $$ Likewise, the other error is a false negative, which we can write analogously as $$ P_{FN} = \mathbb{P}\left( G(\mathbf{X}_n) < c \vert H_1\right) $$ By choosing some acceptable values for either of these errors, we can solve for the other one. The practice is usually to pick a value of $P_{FA}$ and then find the corresponding value of $P_{FN}$. Note that it is traditional in engineering to speak about *detection probability*, which is defined as $$ P_{D} = 1- P_{FN} = \mathbb{P}\left( G(\mathbf{X}_n) > c \mid H_1\right) $$ In other words, this is the probability of declaring $H_1$ when the test exceeds the threshold. This is otherwise known as the *probability of a true detection* or *true-detect*. ## Back to the Coin Flipping Example In our previous maximum likelihood discussion, we wanted to derive an estimator for the *value* of the probability of heads for the coin flipping experiment. For hypthesis testing, we want to ask a softer question: is the probability of heads greater or less than $\nicefrac{1}{2}$? As we just established, this leads to the two hypotheses: $$ H_0 \colon \theta < \frac{1}{2} $$ versus, $$ H_1 \colon \theta > \frac{1}{2} $$ Let's assume we have five observations. Now we need the $G$ function and a threshold $c$ to help pick between the two hypotheses. Let's count the number of heads observed in five observations as our criterion. Thus, we have $$ G(\mathbf{X}_5) := \sum_{i=1}^5 X_i $$ and, suppose further that we pick $H_1$ only if exactly five out of five observations are heads. We'll call this the *all-heads* test. Now, because all of the $X_i$ are random variables, so is $G$ and we must find the corresponding probability mass function for $G$. Assuming the individual coin tosses are independent, the probability of five heads is $\theta^5$. This means that the probability of rejecting the $H_0$ hypothesis (and choosing $H_1$, because there are only two choices here) based on the unknown underlying probability is $\theta^5$. In the parlance, this is known and the *power function* as in denoted by $\beta$ as in $$ \beta(\theta) = \theta^5 $$ Let's get a quick plot this in [Figure](#fig:Hypothesis_testing_001).%matplotlib inline
from matplotlib.pylab import subplots
import numpy as np
fig,ax=subplots()
fig.set_size_inches((6,3))
xi = np.linspace(0,1,50)
_=ax.plot(xi, (xi)**5,'-k',label='all heads')
_=ax.set_xlabel(r'$\theta$',fontsize=22)
_=ax.plot(0.5,(0.5)**5,'ko')
fig.tight_layout()
fig.savefig('fig-statistics/Hypothesis_Testing_001.png')
Power function for the all-heads test. The dark circle indicates the value of the function indicating $\alpha$.
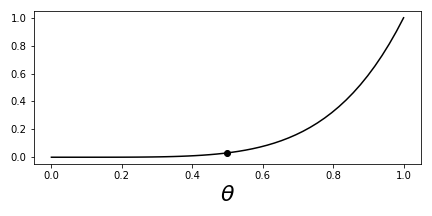
Now, we have the following false alarm probability,
$$ P_{FA} = \mathbb{P}( G(\mathbf{X}_n)= 5 \vert H_0) =\mathbb{P}( \theta^5 \vert H_0) $$Notice that this is a function of $\theta$, which means there are many false alarm probability values that correspond to this test. To be on the conservative side, we'll pick the supremum (i.e., maximum) of this function, which is known as the size of the test, traditionally denoted by $\alpha$,
$$ \alpha = \sup_{\theta \in \Theta_0} \beta(\theta) $$with domain $\Theta_0 = \lbrace \theta < 1/2 \rbrace$ which in our case is
$$ \alpha = \sup_{\theta < \frac{1}{2}} \theta^5 = \left(\frac{1}{2}\right)^5 = 0.03125 $$Likewise, for the detection probability,
$$ \mathbb{P}_{D}(\theta) = \mathbb{P}( \theta^5 \vert H_1) $$which is again a function of the parameter $\theta$. The problem with this test is that the $P_{D}$ is pretty low for most of the domain of $\theta$. For instance, values in the nineties for $P_{D}$ only happen when $\theta > 0.98$. In other words, if the coin produces heads 98 times out of 100, then we can detect $H_1$ reliably. Ideally, we want a test that is zero for the domain corresponding to $H_0$ (i.e., $\Theta_0$) and equal to one otherwise. Unfortunately, even if we increase the length of the observed sequence, we cannot escape this effect with this test. You can try plotting $\theta^n$ for larger and larger values of $n$ to see this.
Majority Vote Test¶
Due to the problems with the detection probability in the all-heads test, maybe we can think of another test that will have the performance we want? Suppose we reject $H_0$ if the majority of the observations are heads. Then, using the same reasoning as above, we have
$$ \beta(\theta) = \sum_{k=3}^5 \binom{5}{k} \theta^k(1-\theta)^{5-k} $$Figure shows the power function for both the majority vote and the all-heads tests.
fig,ax=subplots()
fig.set_size_inches((6,3))
from sympy.abc import theta,k # get some variable symbols
import sympy as S
xi = np.linspace(0,1,50)
expr=S.Sum(S.binomial(5,k)*theta**(k)*(1-theta)**(5-k),(k,3,5)).doit()
_=ax.plot(xi, (xi)**5,'-k',label='all heads')
_=ax.plot(xi, S.lambdify(theta,expr)(xi),'--k',label='majority vote')
_=ax.plot(0.5, (0.5)**5,'ko')
_=ax.plot(0.5, S.lambdify(theta,expr)(0.5),'ko')
_=ax.set_xlabel(r'$\theta$',fontsize=22)
_=ax.legend(loc=0)
fig.tight_layout()
fig.savefig('fig-statistics/Hypothesis_Testing_002.png')
Compares the power function for the all-heads test with that of the majority-vote test.
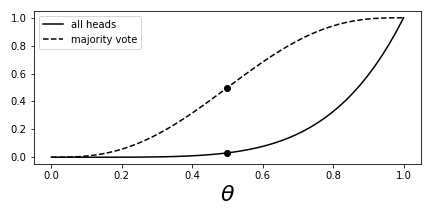
In this case, the new test has size
$$ \alpha = \sup_{\theta < \frac{1}{2}} \theta^{5} + 5 \theta^{4} \left(- \theta + 1\right) + 10 \theta^{3} \left(- \theta + 1\right)^{2} = \frac{1}{2} $$As before we only get to upwards of 90% for detection probability only when the underlying parameter $\theta > 0.75$. Let's see what happens when we consider more than five samples. For example, let's suppose that we have $n=100$ samples and we want to vary the threshold for the majority vote test. For example, let's have a new test where we declare $H_1$ when $k=60$ out of the 100 trials turns out to be heads. What is the $\beta$ function in this case?
$$ \beta(\theta) = \sum_{k=60}^{100} \binom{100}{k} \theta^k(1-\theta)^{100-k} $$This is too complicated to write by hand, but the statistics module in Sympy has all the tools we need to compute this.
from sympy.stats import P, Binomial
theta = S.symbols('theta',real=True)
X = Binomial('x',100,theta)
beta_function = P(X>60)
print (beta_function.subs(theta,0.5)) # alpha
print (beta_function.subs(theta,0.70))
These results are much better than before because the $\beta$ function is much steeper. If we declare $H_1$ when we observe 60 out of 100 trials are heads, then we wrongly declare heads approximately 1.8% of the time. Otherwise, if it happens that the true value for $p>0.7$, we will conclude correctly approximately 97% of the time. A quick simulation can sanity check these results as shown below:
from scipy import stats
rv=stats.bernoulli(0.5) # true p = 0.5
# number of false alarms ~ 0.018
print (sum(rv.rvs((1000,100)).sum(axis=1)>60)/1000.)
The above code is pretty dense so let's unpack it. In the first line, we use
the scipy.stats module to define the
Bernoulli random variable for the coin
flip. Then, we use the rvs method of
the variable to generate 1000 trials of
the experiment where each trial
consists of 100 coin flips. This generates a
$1000 \times 100$ matrix where the
rows are the individual trials and the
columns are the outcomes of each
respective set of 100 coin flips. The
sum(axis=1) part computes the sum across the
columns. Because the values of
the embedded matrix are only 1 or 0 this
gives us the count of flips that
are heads per row. The next >60 part
computes the boolean 1000-long vector of
values that are bigger than 60. The
final sum adds these up. Again, because
the entries in the array are True
or False the sum computes the count of
times the number of heads has
exceeded 60 per 100 coin flips in each of 1000
trials. Then, dividing this
number by 1000 gives a quick approximation of false
alarm probability we
computed above for this case where the true value of
$p=0.5$.
Receiver Operating Characteristic¶
Because the majority vote test is a binary test, we can compute the Receiver Operating Characteristic (ROC) which is the graph of the $(P_{FA}, P_D)$. The term comes from radar systems but is a very general method for consolidating all of these issues into a single graph. Let's consider a typical signal processing example with two hypotheses. In $H_0$, there is noise but no signal present at the receiver,
$$ H_0 \colon X = \epsilon $$where $\epsilon \sim \mathcal{N}(0,\sigma^2)$ represents additive noise. In the alternative hypothesis, there is a deterministic signal at the receiver,
$$ H_1 \colon X = \mu + \epsilon $$Again, the problem is to choose between these two hypotheses. For $H_0$, we have $X \sim \mathcal{N}(0,\sigma^2)$ and for $H_1$, we have $ X \sim \mathcal{N}(\mu,\sigma^2)$. Recall that we only observe values for $x$ and must pick either $H_0$ or $H_1$ from these observations. Thus, we need a threshold, $c$, to compare $x$ against in order to distinguish the two hypotheses. Figure shows the probability density functions under each of the hypotheses. The dark vertical line is the threshold $c$. The gray shaded area is the probability of detection, $P_D$ and the shaded area is the probability of false alarm, $P_{FA}$. The test evaluates every observation of $x$ and concludes $H_0$ if $x<c$ and $H_1$ otherwise.
The two density functions for the $H_0$ and $H_1$ hypotheses. The shaded gray area is the detection probability and the shaded dark gray area is the probability of false alarm. The vertical line is the decision threshold.
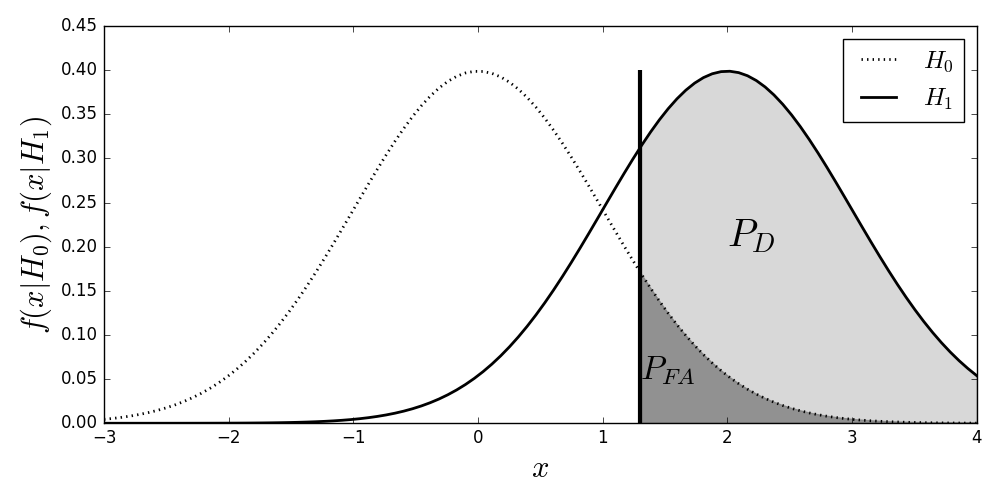 **Programming Tip.**
The shading shown in [Figure](#fig:Hypothesis_testing_003)
comes from
Matplotlib's `fill_between` function. This function has a `where`
keyword
argument to specify which part of the plot to apply shading with
specified
`color` keyword argument. Note there is also a `fill_betweenx`
function that
fills horizontally. The `text` function can place formatted
text
anywhere in the plot and can utilize basic \LaTeX{} formatting.
As we slide
the threshold left and right along the horizontal axis, we naturally change the
corresponding areas under
each of the curves shown in
[Figure](#fig:Hypothesis_testing_003) and thereby
change the values of $P_D$ and
$P_{FA}$. The contour that emerges from sweeping
the threshold this way is the
ROC as shown in [Figure](#fig:Hypothesis_testing_004). This figure also shows
the diagonal line which
corresponds to making decisions based on the flip of a
fair coin. Any
meaningful test must do better than coin flipping so the more the
ROC bows up
to the top left corner of the graph, the better. Sometimes ROCs are
quantified
into a single number called the *area under the curve* (AUC), which
varies from
0.5 to 1.0 as shown. In our example, what separates the two
probability density
functions is the value of $\mu$. In a real situation, this
would be determined
by signal processing methods that include many complicated
trade-offs. The key
idea is that whatever those trade-offs are, the test itself
boils down to the
separation between these two density functions --- good tests
separate the two
density functions and bad tests do not. Indeed, when there is
no separation, we
arrive at the diagonal-line coin-flipping situation we just
discussed.
What values for $P_D$ and $P_{FA}$ are considered *acceptable*
depends on the
application. For example, suppose you are testing for a fatal
disease. It could
be that you are willing to except a relatively high $P_{FA}$
value if that
corresponds to a good $P_D$ because the test is relatively cheap
to administer
compared to the alternative of missing a detection. On the other
hand,
may be a false alarm triggers an expensive response, so that minimizing
these alarms is more important than potentially missing a detection. These
trade-offs can only be determined by the application and design factors.
**Programming Tip.**
The shading shown in [Figure](#fig:Hypothesis_testing_003)
comes from
Matplotlib's `fill_between` function. This function has a `where`
keyword
argument to specify which part of the plot to apply shading with
specified
`color` keyword argument. Note there is also a `fill_betweenx`
function that
fills horizontally. The `text` function can place formatted
text
anywhere in the plot and can utilize basic \LaTeX{} formatting.
As we slide
the threshold left and right along the horizontal axis, we naturally change the
corresponding areas under
each of the curves shown in
[Figure](#fig:Hypothesis_testing_003) and thereby
change the values of $P_D$ and
$P_{FA}$. The contour that emerges from sweeping
the threshold this way is the
ROC as shown in [Figure](#fig:Hypothesis_testing_004). This figure also shows
the diagonal line which
corresponds to making decisions based on the flip of a
fair coin. Any
meaningful test must do better than coin flipping so the more the
ROC bows up
to the top left corner of the graph, the better. Sometimes ROCs are
quantified
into a single number called the *area under the curve* (AUC), which
varies from
0.5 to 1.0 as shown. In our example, what separates the two
probability density
functions is the value of $\mu$. In a real situation, this
would be determined
by signal processing methods that include many complicated
trade-offs. The key
idea is that whatever those trade-offs are, the test itself
boils down to the
separation between these two density functions --- good tests
separate the two
density functions and bad tests do not. Indeed, when there is
no separation, we
arrive at the diagonal-line coin-flipping situation we just
discussed.
What values for $P_D$ and $P_{FA}$ are considered *acceptable*
depends on the
application. For example, suppose you are testing for a fatal
disease. It could
be that you are willing to except a relatively high $P_{FA}$
value if that
corresponds to a good $P_D$ because the test is relatively cheap
to administer
compared to the alternative of missing a detection. On the other
hand,
may be a false alarm triggers an expensive response, so that minimizing
these alarms is more important than potentially missing a detection. These
trade-offs can only be determined by the application and design factors.
The Receiver Operating Characteristic (ROC) corresponding to [Figure](#fig:Hypothesis_testing_003).
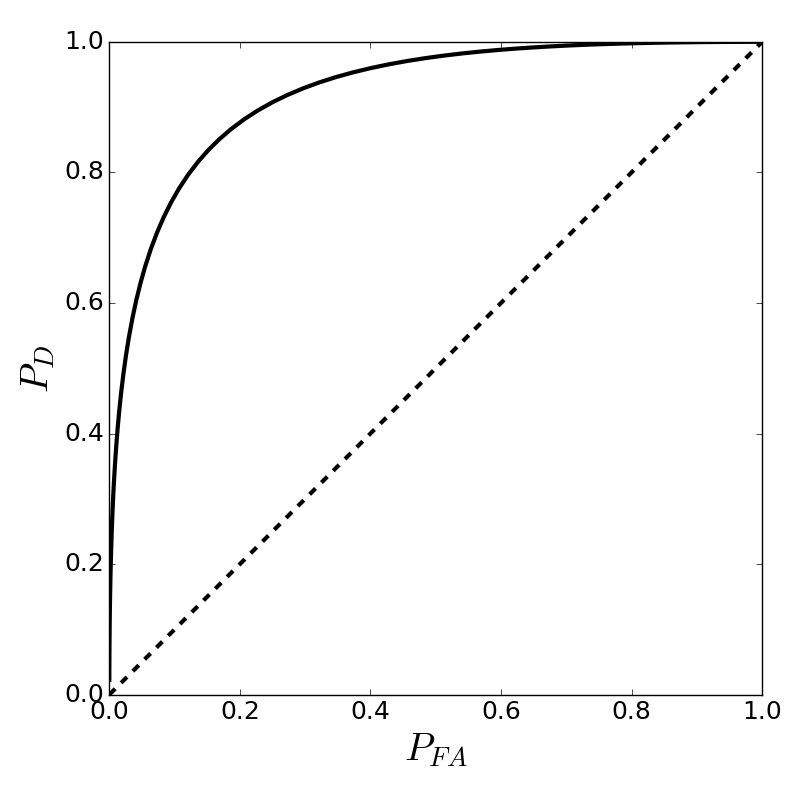
#¶
P-Values
There are a lot of moving parts in hypothesis testing. What we need is a way to consolidate the findings. The idea is that we want to find the minimum level at which the test rejects $H_0$. Thus, the p-value is the probability, under $H_0$, that the test-statistic is at least as extreme as what was actually observed. Informally, this means that smaller values imply that $H_0$ should be rejected, although this doesn't mean that large values imply that $H_0$ should be retained. This is because a large p-value can arise from either $H_0$ being true or the test having low statistical power.
If $H_0$ is true, the p-value is uniformly distributed in the interval $(0,1)$. If $H_1$ is true, the distribution of the p-value will concentrate closer to zero. For continuous distributions, this can be proven rigorously and implies that if we reject $H_0$ when the corresponding p-value is less than $\alpha$, then the probability of a false alarm is $\alpha$. Perhaps it helps to formalize this a bit before computing it. Suppose $\tau(X)$ is a test statistic that rejects $H_0$ as it gets bigger. Then, for each sample $x$, corresponding to the data we actually have on-hand, we define
$$ p(x) = \sup_{\theta \in \Theta_0} \mathbb{P}_{\theta}(\tau(X) > \tau(x)) $$This equation states that the supremum (i.e., maximum) probability that the test statistic, $\tau(X)$, exceeds the value for the test statistic on this particular data ($\tau(x)$) over the domain $\Theta_0$ is defined as the p-value. Thus, this embodies a worst-case scenario over all values of $\theta$. Here's one way to think about this. Suppose you rejected $H_0$, and someone says that you just got lucky and somehow just drew data that happened to correspond to a rejection of $H_0$. What p-values provide is a way to address this by capturing the odds of just a favorable data-draw. Thus, suppose that your p-value is 0.05. Then, what you are showing is that the odds of just drawing that data sample, given $H_0$ is in force, is just 5%. This means that there's a 5% chance that you somehow lucked out and got a favorable draw of data.
Let's make this concrete with an example. Given, the majority-vote rule above, suppose we actually do observe three of five heads. Given the $H_0$, the probability of observing this event is the following:
$$ p(x) =\sup_{\theta \in \Theta_0} \sum_{k=3}^5\binom{5}{k} \theta^k(1-\theta)^{5-k} = \frac{1}{2} $$For the all-heads test, the corresponding computation is the following:
$$ p(x) =\sup_{\theta \in \Theta_0} \theta^5 = \frac{1}{2^5} = 0.03125 $$From just looking at these p-values, you might get the feeling that the second test is better, but we still have the same detection probability issues we discussed above; so, p-values help in summarizing some aspects of our hypothesis testing, but they do not summarize all the salient aspects of the entire situation.
Test Statistics¶
As we have seen, it is difficult to derive good test statistics for hypothesis testing without a systematic process. The Neyman-Pearson Test is derived from fixing a false-alarm value ($\alpha$) and then maximizing the detection probability. This results in the Neyman-Pearson Test,
$$ L(\mathbf{x}) = \frac{f_{X|H_1}(\mathbf{x})}{f_{X|H_0}(\mathbf{x})} \stackrel[H_0]{H_1}{\gtrless} \gamma $$where $L$ is the likelihood ratio and where the threshold $\gamma$ is chosen such that
$$ \int_{x:L(\mathbf{x})>\gamma} f_{X|H_0}(\mathbf{x}) d\mathbf{x}=\alpha $$The Neyman-Pearson Test is one of a family of tests that use the likelihood ratio.
Example. Suppose we have a receiver and we want to distinguish whether just noise ($H_0$) or signal pluse noise ($H_1$) is received. For the noise-only case, we have $x\sim \mathcal{N}(0,1)$ and for the signal pluse noise case we have $x\sim \mathcal{N}(1,1)$. In other words, the mean of the distribution shifts in the presence of the signal. This is a very common problem in signal processing and communications. The Neyman-Pearson Test then boils down to the following,
$$ L(x)= e^{-\frac{1}{2}+x}\stackrel[H_0]{H_1}{\gtrless}\gamma $$Now we have to find the threshold $\gamma$ that solves the maximization problem that characterizes the Neyman-Pearson Test. Taking the natural logarithm and re-arranging gives,
$$ x\stackrel[H_0]{H_1}{\gtrless} \frac{1}{2}+\log\gamma $$The next step is find $\gamma$ corresponding to the desired $\alpha$ by computing it from the following,
$$ \int_{1/2+\log\gamma}^{\infty} f_{X|H_0}(x)dx = \alpha $$For example, taking $\alpha=1/100$, gives $\gamma\approx 6.21$. To summarize the test in this case, we have,
$$ x\stackrel[H_0]{H_1}{\gtrless} 2.32 $$Thus, if we measure $X$ and see that its value exceeds the threshold above, we declare $H_1$ and otherwise declare $H_0$. The following code shows how to solve this example using Sympy and Scipy. First, we set up the likelihood ratio,
import sympy as S
from sympy import stats
s = stats.Normal('s',1,1) # signal+noise
n = stats.Normal('n',0,1) # noise
x = S.symbols('x',real=True)
L = stats.density(s)(x)/stats.density(n)(x)
Next, to find the $\gamma$ value,
g = S.symbols('g',positive=True) # define gamma
v=S.integrate(stats.density(n)(x),
(x,S.Rational(1,2)+S.log(g),S.oo))
Programming Tip.
Providing additional information regarding the Sympy
variable by using the
keyword argument positive=True helps the internal
simplification algorithms
work faster and better. This is especially useful when
dealing with complicated
integrals that involve special functions. Furthermore,
note that we used the
Rational function to define the 1/2 fraction, which is
another way of
providing hints to Sympy. Otherwise, it's possible that the
floating-point
representation of the fraction could disguise the simple
fraction and
thereby miss internal simplification opportunities.
We want to
solve for g in the above expression. Sympy has some
built-in numerical solvers
as in the following,
print (S.nsolve(v-0.01,3.0)) # approx 6.21
Note that in this situation it is better to use the numerical
solvers because
Sympy solve may grind along for a long time to
resolve this.
Generalized¶
Likelihood Ratio Test
The likelihood ratio test can be generalized using the following statistic,
$$ \Lambda(\mathbf{x})= \frac{\sup_{\theta\in\Theta_0} L(\theta)}{\sup_{\theta\in\Theta} L(\theta)}=\frac{L(\hat{\theta}_0)}{L(\hat{\theta})} $$where $\hat{\theta}_0$ maximizes $L(\theta)$ subject to $\theta\in\Theta_0$ and $\hat{\theta}$ is the maximum likelihood estimator. The intuition behind this generalization of the Likelihood Ratio Test is that the denomimator is the usual maximum likelihood estimator and the numerator is the maximum likelihood estimator, but over a restricted domain ($\Theta_0$). This means that the ratio is always less than unity because the maximum likelihood estimator over the entire space will always be at least as maximal as that over the more restricted space. When this $\Lambda$ ratio gets small enough, it means that the maximum likelihood estimator over the entire domain ($\Theta$) is larger which means that it is safe to reject the null hypothesis $H_0$. The tricky part is that the statistical distribution of $\Lambda$ is usually eye-wateringly difficult. Fortunately, Wilks Theorem says that with sufficiently large $n$, the distribution of $-2\log\Lambda$ is approximately chi-square with $r-r_0$ degrees of freedom, where $r$ is the number of free parameters for $\Theta$ and $r_0$ is the number of free parameters in $\Theta_0$. With this result, if we want an approximate test at level $\alpha$, we can reject $H_0$ when $-2\log\Lambda \ge \chi^2_{r-r_0}(\alpha)$ where $\chi^2_{r-r_0}(\alpha)$ denotes the $1-\alpha$ quantile of the $\chi^2_{r-r_0}$ chi-square distribution. However, the problem with this result is that there is no definite way of knowing how big $n$ should be. The advantage of this generalized likelihood ratio test is that it can test multiple hypotheses simultaneously, as illustrated in the following example. Example. Let's return to our coin-flipping example, except now we have three different coins. The likelihood function is then,
$$ L(p_1,p_2,p_3) = \texttt{binom}(k_1;n_1,p_1)\texttt{binom}(k_2;n_2,p_2)\texttt{binom}(k_3;n_3,p_3) $$where $\texttt{binom}$ is the binomial distribution with the given parameters. For example,
$$ \texttt{binom}(k;n,p) =\sum_{k=0}^n \binom{n}{k} p^k(1-p)^{n-k} $$The null hypothesis is that all three coins have the same probability of heads, $H_0:p=p_1=p_2=p_3$. The alternative hypothesis is that at least one of these probabilites is different. Let's consider the numerator of the $\Lambda$ first, which will give us the maximum likelihood estimator of $p$. Because the null hypothesis is that all the $p$ values are equal, we can just treat this as one big binomial distribution with $n=n_1+n_2+n_3$ and $k=k_1+k_2+k_3$ is the total number of heads observed for any coin. Thus, under the null hypothesis, the distribution of $k$ is binomial with parameters $n$ and $p$. Now, what is the maximum likelihood estimator for this distribution? We have worked this problem before and have the following,
$$ \hat{p}_0= \frac{k}{n} $$In other words, the maximum likelihood estimator under the null hypothesis is the proportion of ones observed in the sequence of $n$ trials total. Now, we have to substitute this in for the likelihood under the null hypothesis to finish the numerator of $\Lambda$,
$$ L(\hat{p}_0,\hat{p}_0,\hat{p}_0) = \texttt{binom}(k_1;n_1,\hat{p}_0)\texttt{binom}(k_2;n_2,\hat{p}_0)\texttt{binom}(k_3;n_3,\hat{p}_0) $$For the denomimator of $\Lambda$, which represents the case of maximizing over the entire space, the maximum likelihood estimator for each separate binomial distribution is likewise,
$$ \hat{p}_i= \frac{k_i}{n_i} $$which makes the likelihood in the denominator the following,
$$ L(\hat{p}_1,\hat{p}_2,\hat{p}_3) = \texttt{binom}(k_1;n_1,\hat{p}_1)\texttt{binom}(k_2;n_2,\hat{p}_2)\texttt{binom}(k_3;n_3,\hat{p}_3) $$for each of the $i\in \lbrace 1,2,3 \rbrace$ binomial distributions. Then, the $\Lambda$ statistic is then the following,
$$ \Lambda(k_1,k_2,k_3) = \frac{L(\hat{p}_0,\hat{p}_0,\hat{p}_0)}{L(\hat{p}_1,\hat{p}_2,\hat{p}_3)} $$Wilks theorems states that $-2\log\Lambda$ is chi-square distributed. We can compute this example with the statistics tools in Sympy and Scipy.
from scipy.stats import binom, chi2
import numpy as np
# some sample parameters
p0,p1,p2 = 0.3,0.4,0.5
n0,n1,n2 = 50,180,200
brvs= [ binom(i,j) for i,j in zip((n0,n1,n2),(p0,p1,p2))]
def gen_sample(n=1):
'generate samples from separate binomial distributions'
if n==1:
return [i.rvs() for i in brvs]
else:
return [gen_sample() for k in range(n)]
Programming Tip.
Note the recursion in the definition of the gen_sample
function where a
conditional clause of the function calls itself. This is a
quick way to reusing
code and generating vectorized output. Using np.vectorize
is another way, but
the code is simple enough in this case to use the
conditional clause. In
Python, it is generally bad for performance to have code
with nested recursion
because of how the stack frames are managed. However,
here we are only
recursing once so this is not an issue.
Next, we compute the logarithm of the numerator of the $\Lambda$ statistic,
np.random.seed(1234)
k0,k1,k2 = gen_sample()
print (k0,k1,k2)
pH0 = sum((k0,k1,k2))/sum((n0,n1,n2))
numer = np.sum([np.log(binom(ni,pH0).pmf(ki))
for ni,ki in
zip((n0,n1,n2),(k0,k1,k2))])
print (numer)
Note that we used the null hypothesis estimate for the $\hat{p}_0$. Likewise, for the logarithm of the denominator we have the following,
denom = np.sum([np.log(binom(ni,pi).pmf(ki))
for ni,ki,pi in
zip((n0,n1,n2),(k0,k1,k2),(p0,p1,p2))])
print (denom)
Now, we can compute the logarithm of the $\Lambda$ statistic as follows and see what the corresponding value is according to Wilks theorem,
chsq=chi2(2)
logLambda =-2*(numer-denom)
print (logLambda)
print (1- chsq.cdf(logLambda))
Because the value reported above is less than the 5% significance level, we reject the null hypothesis that all the coins have the same probability of heads. Note that there are two degrees of freedom because the difference in the number of parameters between the null hypothesis ($p$) and the alternative ($p_1,p_2,p_3$) is two. We can build a quick Monte Carlo simulation to check the probability of detection for this example using the following code, which is just a combination of the last few code blocks,
c= chsq.isf(.05) # 5% significance level
out = []
for k0,k1,k2 in gen_sample(100):
pH0 = sum((k0,k1,k2))/sum((n0,n1,n2))
numer = np.sum([np.log(binom(ni,pH0).pmf(ki))
for ni,ki in
zip((n0,n1,n2),(k0,k1,k2))])
denom = np.sum([np.log(binom(ni,pi).pmf(ki))
for ni,ki,pi in
zip((n0,n1,n2),(k0,k1,k2),(p0,p1,p2))])
out.append(-2*(numer-denom)>c)
print (np.mean(out)) # estimated probability of detection
The above simulation shows the estimated probability of detection, for this set of example parameters. This relative low probability of detection means that while the test is unlikely (i.e., at the 5% significance level) to mistakenly pick the null hypothesis, it is likewise missing many of the $H_1$ cases (i.e., low probability of detection). The trade-off between which is more important is up to the particular context of the problem. In some situations, we may prefer additional false alarms in exchange for missing fewer $H_1$ cases.
#¶
Permutation Test
The Permutation Test is good way to test whether or not samples samples come from the same distribution. For example, suppose that
$$ X_1, X_2, \ldots, X_m \sim F $$and also,
$$ Y_1, Y_2, \ldots, Y_n \sim G $$That is, $Y_i$ and $X_i$ come from different distributions. Suppose we have some test statistic, for example
$$ T(X_1,\ldots,X_m,Y_1,\ldots,Y_n) = \vert\overline{X}-\overline{Y}\vert $$Under the null hypothesis for which $F=G$, any of the $(n+m)!$ permutations are equally likely. Thus, suppose for each of the $(n+m)!$ permutations, we have the computed statistic,
$$ \lbrace T_1,T_2,\ldots,T_{(n+m)!} \rbrace $$Then, under the null hypothesis, each of these values is equally likely. The distribution of $T$ under the null hypothesis is the permutation distribution that puts weight $1/(n+m)!$ on each $T$-value. Suppose $t_o$ is the observed value of the test statistic and assume that large $T$ rejects the null hypothesis, then the p-value for the permutation test is the following,
$$ P(T>t_o)= \frac{1}{(n+m)!} \sum_{j=1}^{(n+m)!} I(T_j>t_o) $$where $I()$ is the indicator function. For large $(n+m)!$, we can sample randomly from the set of all permutations to estimate this p-value. Example. Let's return to our coin-flipping example from last time, but now we have only two coins. The hypothesis is that both coins have the same probability of heads. We can use the built-in function in Numpy to compute the random permutations.
x=binom(10,0.3).rvs(5) # p=0.3
y=binom(10,0.5).rvs(3) # p=0.5
z = np.hstack([x,y]) # combine into one array
t_o = abs(x.mean()-y.mean())
out = [] # output container
for k in range(1000):
perm = np.random.permutation(z)
T=abs(perm[:len(x)].mean()-perm[len(x):].mean())
out.append((T>t_o))
print ('p-value = ', np.mean(out))
Note that the size of total permutation space is $8!=40320$ so we are taking relatively few (i.e., 100) random permutations from this space.
Wald Test¶
The Wald Test is an asympotic test. Suppose we have $H_0:\theta=\theta_0$ and otherwise $H_1:\theta\ne\theta_0$, the corresponding statistic is defined as the following,
$$ W=\frac{\hat{\theta}_n-\theta_0}{\texttt{se}} $$where $\hat{\theta}$ is the maximum likelihood estimator and $\texttt{se}$ is the standard error,
$$ \texttt{se} = \sqrt{\mathbb{V}(\hat{\theta}_n)} $$Under general conditions, $W\overset{d}{\to} \mathcal{N}(0,1)$. Thus, an asympotic test at level $\alpha$ rejects when $\vert W\vert> z_{\alpha/2}$ where $z_{\alpha/2}$ corresponds to $\mathbb{P}(\vert Z\vert>z_{\alpha/2})=\alpha$ with $Z \sim \mathcal{N}(0,1)$. For our favorite coin-flipping example, if $H_0:\theta=\theta_0$, then
$$ W = \frac{\hat{\theta}-\theta_0}{\sqrt{\hat{\theta}(1-\hat{\theta})/n}} $$We can simulate this using the following code at the usual 5% significance level,
from scipy import stats
theta0 = 0.5 # H0
k=np.random.binomial(1000,0.3)
theta_hat = k/1000. # MLE
W = (theta_hat-theta0)/np.sqrt(theta_hat*(1-theta_hat)/1000)
c = stats.norm().isf(0.05/2) # z_{alpha/2}
print (abs(W)>c) # if true, reject H0
This rejects $H_0$ because the true $\theta=0.3$ and the null hypothesis is that $\theta=0.5$. Note that $n=1000$ in this case which puts us well inside the asympotic range of the result. We can re-do this example to estimate the detection probability for this example as in the following code,
theta0 = 0.5 # H0
c = stats.norm().isf(0.05/2.) # z_{alpha/2}
out = []
for i in range(100):
k=np.random.binomial(1000,0.3)
theta_hat = k/1000. # MLE
W = (theta_hat-theta0)/np.sqrt(theta_hat*(1-theta_hat)/1000.)
out.append(abs(W)>c) # if true, reject H0
print (np.mean(out)) # detection probability
Testing Multiple Hypotheses¶
Thus far, we have focused primarily on two competing hypotheses. Now, we consider multiple comparisons. The general situation is the following. We test the null hypothesis against a sequence of $n$ competing hypotheses $H_k$. We obtain p-values for each hypothesis so now we have multiple p-values to consider $\lbrace p_k \rbrace$. To boil this sequence down to a single criterion, we can make the following argument. Given $n$ independent hypotheses that are all untrue, the probability of getting at least one false alarm is the following,
$$ P_{FA} = 1-(1-p_0)^n $$where $p_0$ is the individual p-value threshold (say, 0.05). The problem here is that $P_{FA}\rightarrow 1$ as $n\rightarrow\infty$. If we want to make many comparisons at once and control the overall false alarm rate the overall p-value should be computed under the assumption that none of the competing hypotheses is valid. The most common way to address this is with the Bonferroni correction which says that the individual significance level should be reduced to $p/n$. Obviously, this makes it much harder to declare significance for any particular hypothesis. The natural consequence of this conservative restriction is to reduce the statistical power of the experiment, thus making it more likely the true effects will be missed.
In 1995, Benjamini and Hochberg devised a simple method that tells which p-values are statistically significant. The procedure is to sort the list of p-values in ascending order, choose a false-discovery rate (say, $q$), and then find the largest p-value in the sorted list such that $p_k \le k q/n$, where $k$ is the p-value's position in the sorted list. Finally, declare that $p_k$ value and all the others less than it statistically significant. This procedure guarantees that the proportion of false-positives is less than $q$ (on average). The Benjamini-Hochberg procedure (and its derivatives) is fast and effective and is widely used for testing hundreds of primarily false hypotheses when studying genetics or diseases. Additionally, this procedure provides better statistical power than the Bonferroni correction.
Fisher Exact Test¶
$$ \begin{table}[] \centering \caption{Example Contingency Table} \label{tab:contingencyTable} \tag{2} \begin{tabular}{lllll} \cline{1-4} \multicolumn{1}{|l|}{} & \multicolumn{1}{l|}{Infection} & \multicolumn{1}{l|}{No infection} & \multicolumn{1}{l|}{Total} & \\ \cline{1-4} \multicolumn{1}{|l|}{Male} & \multicolumn{1}{c|}{13} & \multicolumn{1}{c|}{11} & \multicolumn{1}{c|}{24} & \\ \cline{1-4} \multicolumn{1}{|l|}{Female} & \multicolumn{1}{c|}{12} & \multicolumn{1}{c|}{1} & \multicolumn{1}{c|}{13} & \\ \cline{1-4} \multicolumn{1}{|l|}{Total} & \multicolumn{1}{c|}{25} & \multicolumn{1}{c|}{12} & \multicolumn{1}{c|}{37} & \\ \cline{1-4} \end{tabular} \end{table} $$Contingency tables represent the partitioning of a sample population of two categories between two different classifications as shown in the following Table 2. The question is whether or not the observed table corresponds to a random partition of the sample population, constrained by the marginal sums. Note that because this is a two-by-two table, a change in any of the table entries automatically affects all of the other terms because of the row and column sum constraints. This means that equivalent questions like "Under a random partition, what is the probability that a particular table entry is at least as large as a given value?" can be meaningfully posed.
The Fisher Exact Test addresses this question. The idea is to compute the probability of a particular entry of the table, conditioned upon the marginal row and column sums,
$$ \mathbb{P}(X_{i,j}\vert r_1,r_2,c_1,c_2) $$where $X_{i,j}$ is $(i,j)$ table entry, $r_1$ represents the sum of the first row, $r_2$ represents the sum of the second row, $c_1$ represents the sum of the first column, and $c_2$ is the sum of the second column. This probability is given by the hypergeometric distribution. Recall that the hypergeometric distribution gives the probability of sampling (without replacement) $k$ items from a population of $N$ items consisting of exactly two different kinds of items,
$$ \mathbb{P}(X=k) = \frac{\binom{K}{k}\binom{N-K}{n-k}}{\binom{N}{n}} $$where $N$ is the population size, $K$ is the total number of possible favorable draws, $n$ is the number of draws, and $k$ is the number of observed favorable draws. With the corresponding identification of variables, the hypergeometric distribution gives the desired conditional probability: $K=r_1, k=x, n= c_1, N=r_1+r_2$.
In the example of the Table 2, the
probability for
$x=13$ male infections among a population of $r_1=24$ males in a
total
population of $c_1=25$ infected persons, including $r_2=13$ females. The
scipy.stats module has the Fisher Exact Test implemented as shown below,
import scipy.stats
table = [[13,11],[12,1]]
odds_ratio, p_value=scipy.stats.fisher_exact(table)
print(p_value)
The default for scipy.stats.fisher_exact is the two-sided
test. The following
result is for the less option,
import scipy.stats
odds_ratio, p_value=scipy.stats.fisher_exact(table,alternative='less')
print(p_value)
This means that the p-value is computed by summing over the
probabilities of
contingency tables that are less extreme than the
given table. To undertand
what this means, we can use
the scipy.stats.hypergeom function to compute the
probabilities of
these with the number of infected men is less than or equal to
13.
hg = scipy.stats.hypergeom(37, 24, 25)
probs = [(hg.pmf(i)) for i in range(14)]
print (probs)
print(sum(probs))
This is the same as the prior p-value result we obtained from
scipy.stats.fisher_exact. Another option is greater which derives from the
following analogous summation,
odds_ratio, p_value=scipy.stats.fisher_exact(table,alternative='greater')
probs = [hg.pmf(i) for i in range(13,25)]
print(probs)
print(p_value)
print(sum(probs))
Finally, the two-sided version excludes those individual table probabilities that are less that of the given table
_,p_value=scipy.stats.fisher_exact(table)
probs = [ hg.pmf(i) for i in range(25) ]
print(sum(i for i in probs if i<= hg.pmf(13)))
print(p_value)
Thus, for this particular contingency table, we could reasonably conclude that 13 infected males in this total population is statistically significant with a p-value less than five percent.
Performing this kind of analysis for tables
larger than 2x2 easily becomes
computationally challenging due to the nature
of the underlying combinatorics and
usually requires specialized
approximations.
In this section, we discussed the structure of statistical hypothesis testing and defined the various terms that are commonly used for this process, along with the illustrations of what they mean in our running coin-flipping example. From an engineering standpoint, hypothesis testing is not as common as confidence-intervals and point estimates. On the other hand, hypothesis testing is very common in social and medical science, where one must deal with practical constraints that may limit the sample size or other aspects of the hypothesis testing rubric. In engineering, we can usually have much more control over the samples and models we employ because they are typically inanimate objects that can be measured repeatedly and consistently. This is obviously not so with human studies, which generally have other ethical and legal considerations.